Positional Encoding in Transformers
Why even use Transformers ?
Recurrent Networks are by design able to process sequential data much better than traditional feedforward neural networks. However, due to the recurrence relation, RNNs suffer from Vanishing Gradient when processing longer sequences.
This limits the context size of RNNs.
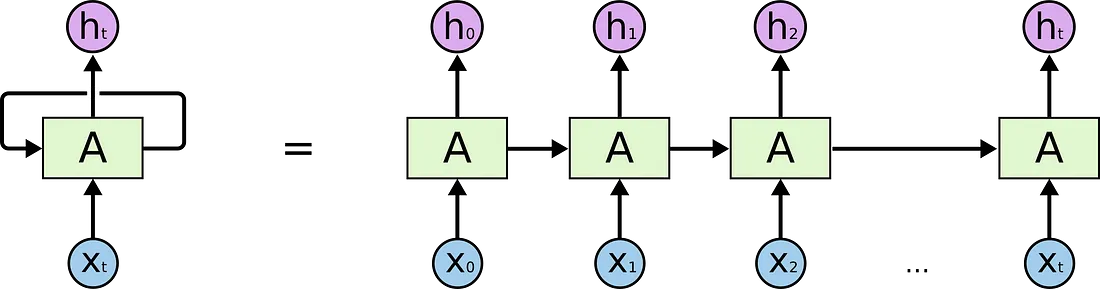
Dealing with one token/word at a time step also makes RNNs painfully slow to train, but this makes sure the model keeps notes of the order of words it is processing.
Transformers do not make use of any architectural relations (no notion of word order), and the model does not have any sense of position/order of the tokens/words being processed. They take all the embeddings into processing at once, vastly improving it’s parallelization potential (and therefore speeding things up), the downside is that they lose critical information related to order of words in our sequence.
Why do positions matter ?
NLP tasks are dependent on the order of words to a great extent, hence it is crucial to supply some context to the model as well.
To soak in context and to analyze relations with neighbouring words, we make use of positional encoding; describing the position of a token by a unique representation.
Context of words affect its meaning. Example :
- Kashmir Apples are in great demand. due to their superior vitamin content.
- Apple is an American Multinational Corporation, known for innovative products for personal computing devices.
The word “Apple” has very different meanings, which can only be interpreted based on the context.
Our representation has to be “rich and deeper” to incorporate information that blends in the context.
Why not use index value ? Why don’t we assign the 1ˢᵗword P₀ , 2ⁿᵈ word P₁ and so on….
- This distorts the embedding values for tokens that appear late in the sequence, giving them a higher value. This high value may not indicate anything meaningful, impacting our learning.
- For extremely long sequences, the index can grow to a large number which the model might confuse with a very large input, causing other issues like gradient overflow.
- Our model can face examples with sequence length greater than what it had observed in the training set. In addition, the model may not have seen any sample with a specific length, which hurts generalization,
- Having a length-related encoding scheme makes the process dependent on the length of the sequence. This becomes an issue as sequences by nature are of varying length.
Each position is mapped to a vector, and the output of the positional layer is a matrix; wherein each row represents an encoded object of the sequence summed with its positional information { NOTE : this information is not concatenated }.
Requirements of the encoding
Does not depend on any characteristics of the input, be it length or semantic meaning.
Distance of embeddings between time steps should be consistent across sentences with different lengths. That is only possible when embeddings are obtained by using something fundamental, in this case sinusoidal functions.
How to compute this encoding ?
Instead of a single number to denote the position, transformers make use of multi-dimensional vectors. This encoding is supplied as a part of the input, equipping each token with information about its position in the sequence.

pos : position of the word/token in the sequence
i : refers to one of the embedding dimensions
d : size of position embedding, equal to size of word embeddings
While “d“ is fixed, pos and i vary
A sinusoid is repetitive in nature, and therefore the positional encodings might repeat after a few token right ?
Take note of the “i” component of the sinusoid. It can be understood as a component which affects the frequency of our embedding function. As “i” varies, we get different values for different dimensions.

If two points are close by on the curve, they will remain close even at slightly higher frequencies. The difference is noticeable only at high frequency curves, where even for small variations, the output can wildly differ. leading to very different vectors.
In reality, both sin and cosine functions are used to generate embeddings.
Even positions : sin
Odd positions : cosine
To add the positional embedding to our input embedding, we must note that the dimensions for the two have to be compatible. Hence “d” for the positional encoding is equal to the “d” of the word embedding. In the original paper, d is set at 512.
To avoid losing this position/order information deeper down the network, transformers make use of residual connections, giving deeper layers access to this encoding.
Another advantage of using sinusoidal functions to create embeddings is that these can be used even for sequences larger than the ones seen during training, as extrapolation is simple.
This can be simply written as :
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_sequence_length):
super().__init__()
self.max_sequence_length = max_sequence_length
self.d_model = d_model
def forward(self):
even_i = torch.arange(0, self.d_model, 2).float()
denominator = torch.pow(10000, even_i/self.d_model)
position = torch.arange(self.max_sequence_length).reshape(self.max_sequence_length, 1)
even_PE = torch.sin(position / denominator)
odd_PE = torch.cos(position / denominator)
stacked = torch.stack([even_PE, odd_PE], dim=2)
PE = torch.flatten(stacked, start_dim=1, end_dim=2)
return PE
For more on Transformers, I’ll publish another blog in a day or two !!
Checkout more on my Twitter page
References