Loss function for the algorithm?
loss function in machine learning is simply a measure of how different the predicted value is from the actual value. The quadratic Loss Function calculates the loss or error in our model. It can be defined as:
\[\text{SSR} = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2\]Minimizing it by finding the partial derivative of L, equating it to 0, and then finding an expression for m and c. After we do the math, we are left with these equations:
\[c = \hat{y} - m\hat{x} \\ m = \frac{\sum_{i=1}^{n} (x_i - \hat{x})~(y_i - \hat{y})} {\sum_{i=1}^{n} (x_i - \hat{x})^2}\]Least Squares using matrices
The idea is to find the set of parameters ($\theta$) such that: $ X \theta = y $ where,
X: input data with dimensions (n,m),
Θ: parameters with dimensions (m,1),
y: output data with dimensions (n,1),
n: number of samples,
m: number of features
The parameter matrix \theta can be directly determined by multiplying both sides of the equation with the inverse of X, as : $ \theta = X^{-1}y $
But because X might be a non-square matrix, its inverse may not be defined.
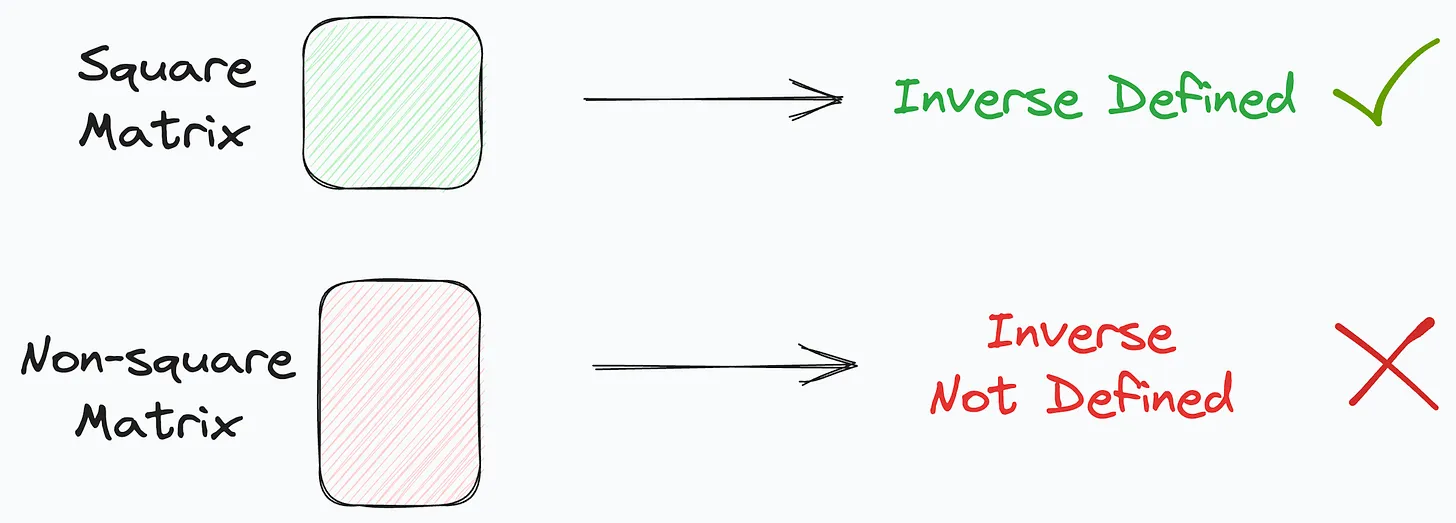
To resolve this, first, we multiply with the transpose of X on both sides, as : $ X^{T}X\theta = X^{T}y $
This makes the product of X with its transpose, a square matrix.
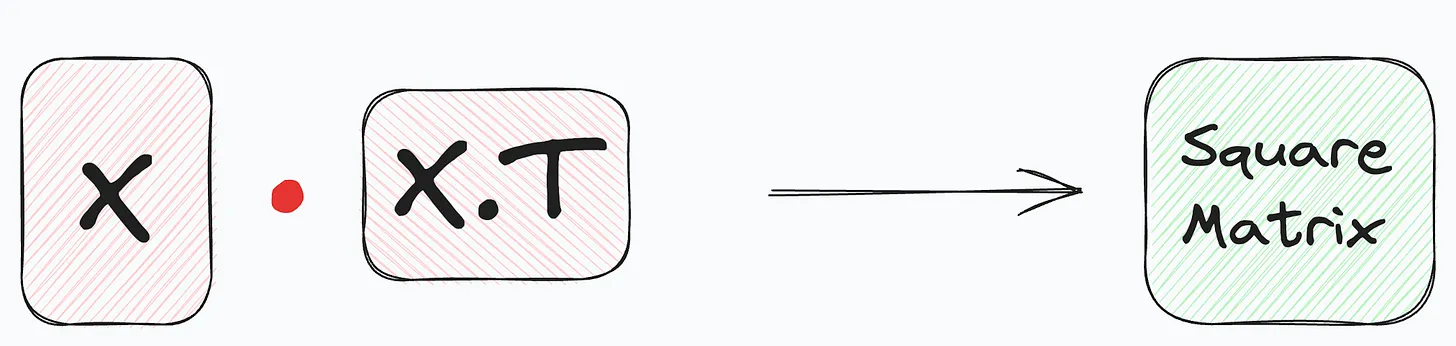
The obtained matrix, being square, can be inverted. Taking the collective inverse of the product to get the following:
\[\theta = ( X^{T}~X ) ^ {-1}~X^{T}~y\]No randomness. Thus, it will always return the same solution, which is also optimal.
This is precisely what the Linear Regression class of Sklearn implements, Instead of gradient descent.
Head over here to see projects being
mentored over at BSoC
, which is a programme ran by the Programming Club at IIIT Jabalpur, aimed at freshmen transitioning over to their sophomore year, with projects.